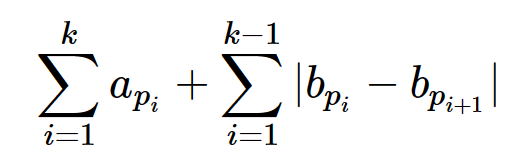比赛链接：Dashboard - Codeforces Round 932 (Div. 2) - Codeforces

C

题意：给出一个数组包含 $n$ 个元素，每个元素包含 $a$、$b$ 两个元素，在这个数组中找出最多的元素并令其下标为 $p_1,…,p_k$ ，使得：

不超过 $l$ 。$n^2\leq 2 \times 10^6$

  1. 把数组按照 $b$ 从大到小排序后，$n^2$ 遍历 $b$ 项的开头 $st$ 与结尾 $ed$ ，可以证得当 $b$ 降序排列时得到的和最小。
  2. 用 $multiset$ 维护 $st$ 与 $ed$ 之间的 $a$ 的最大值。

不用担心在multiset中将ed元素的a值删除，因为删除后等效于ed位置提前，且b项的值还变大了，故不会影响答案统计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
using namespace std;
// #define int long long

bool cmp(pair<int,int>x,pair<int,int>y)
{
    return x.second>y.second;
}

void solve()
{
    int n,l;
    cin>>n>>l;
    pair<int,int>a[n+5];
    for(int i=1;i<=n;i++)
    {
        cin>>a[i].first>>a[i].second;
    }
    sort(a+1,a+n+1,cmp);
    
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        multiset<int>q;
        int sum=0;
        for(int j=i;j<=n;j++)
        {
            sum+=a[j].first;
            q.insert(a[j].first);
            while(q.size() && sum+a[i].second-a[j].second>l)
            {
                int mx=*q.rbegin();
                sum-=mx;
                q.erase(q.find(mx));
            }
            ans=max(ans,(int)q.size());
        }
    }
    cout<<ans<<endl;
    
}

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin>>t;
    while(t--)solve();
    return 0;
}

math

D

题意：给出一个大小为 $n$ 的集合 $s$ 和整数 $c$ 。对于这个集合，计算出 $0\leq x\leq y\leq c$ ， $x+y$ 、$y-x$ 不包含在集合 $s$ 中的整数对 $(x,y)$ 的数量。

考虑容斥的思想，$ans(x,y)=cnt(x,y)-cnt(x,y,x+y\in s)-cnt(x,y,y-x\in s)+cnt(x,y,x+y\in s,y-x\in s)$。

  1. $cnt(x,y)=C_{c+1}^{2}+c+1=\frac{(c+1)(c+2)}{2}$
  2. $cnt(x,y,x+y\in s)=\lfloor \frac{a_{i}}{2}\rfloor+1 $
  3. $cnt(x,y,y-x\in s)=c-a_{i}+1$
  4. $cnt(x,y,x+y\in s,y-x\in s)=\frac{even(even+1)}{2}+\frac{ood(odd+1)}{2}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
#define int long long 
signed main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,c;
        cin>>n>>c;
        int a[n+5];
        int ev=0;
        int od=0;
        int ans=(c+1)*(c+2)/2;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
            if(a[i]%2==0)ev++;
            else od++;
            ans-=a[i]/2+1;
            ans-=c-a[i]+1;
        }
        ans+=ev*(ev+1)/2+od*(od+1)/2;
        cout<<ans<<endl;
    }
    return 0;
}

math